|
Mathematical
theory behind the quality and efficiency of digitised sound and pictures
has taken a step forward with research from the City University of Hong
Kong.
 The scientist
attributed with being the Father of the Digital Age, American Claude Shannon,
wrote the blueprint for digital communications in the 1940s. But, said
the CityU project’s Principal Investigator, Dr Ding-xuan Zhou, the
theory could not be implemented. The scientist
attributed with being the Father of the Digital Age, American Claude Shannon,
wrote the blueprint for digital communications in the 1940s. But, said
the CityU project’s Principal Investigator, Dr Ding-xuan Zhou, the
theory could not be implemented.
 Shannon’s
idea was that pictures and sound could be transmitted more efficiently,
or digitally, if only samples from certain points of the media were used
to make up a digital signal. Shannon’s
idea was that pictures and sound could be transmitted more efficiently,
or digitally, if only samples from certain points of the media were used
to make up a digital signal.
 Although the
resulting picture or sound was different from the original, very little
information would be lost. Although the
resulting picture or sound was different from the original, very little
information would be lost.
 “What scientists
have been working on since then is to make the difference as small as possible,”
said Dr Zhou. “What scientists
have been working on since then is to make the difference as small as possible,”
said Dr Zhou.
 With sound,
for example, values can be taken at one second intervals, or at other convenient
integer points and, when recomposed, it will be like the original whole
signal. With sound,
for example, values can be taken at one second intervals, or at other convenient
integer points and, when recomposed, it will be like the original whole
signal.
 “For images,
values are similarly taken at integer points, or decomposed, and when recomposed
they look very much like the original image. “For images,
values are similarly taken at integer points, or decomposed, and when recomposed
they look very much like the original image.
 “The benefit
is that it takes less data to represent a lot of information,” said
Dr Zhou. “You want to use the least amount of data as possible but
you want the image or the sound to be as close to the original as possible. “The benefit
is that it takes less data to represent a lot of information,” said
Dr Zhou. “You want to use the least amount of data as possible but
you want the image or the sound to be as close to the original as possible.
 “When you
use this idea, of course you lose information. Even though you consider
the sound or image to be identical, it isn’t.” “When you
use this idea, of course you lose information. Even though you consider
the sound or image to be identical, it isn’t.”
 The main problem
with Shannon’s theorem, he said, was that the time element in the signal
processing was infinite. It needed to be finite, or capture values at a
particular time. The main problem
with Shannon’s theorem, he said, was that the time element in the signal
processing was infinite. It needed to be finite, or capture values at a
particular time.
 Work in the
1970s used different “quadrature mirror” filters in so-called
sub-band coding schemes, which divided signals into smaller bands of frequencies,
therefore making them easier to process. Work in the
1970s used different “quadrature mirror” filters in so-called
sub-band coding schemes, which divided signals into smaller bands of frequencies,
therefore making them easier to process.
 The quadrature
mirror filters still did not produce a perfect result if the filters are
required to have finite impulse responses, said Dr Zhou. Too much signal
information was lost. New types of filters were devised with the latest
conjugate quadrature filters eliminating any information loss. The quadrature
mirror filters still did not produce a perfect result if the filters are
required to have finite impulse responses, said Dr Zhou. Too much signal
information was lost. New types of filters were devised with the latest
conjugate quadrature filters eliminating any information loss.
 Dr Zhou’s
research has centred on the latest schemes of sub-band coding using conjugate
quadrature filters and to show their foundation for wavelet analysis in
applied mathematics. Dr Zhou’s
research has centred on the latest schemes of sub-band coding using conjugate
quadrature filters and to show their foundation for wavelet analysis in
applied mathematics.
 “As well
as knowing the scheme is perfect, we can show mathematically that it is
correct.” In addition to revealing the mathematical foundation of the
schemes, Dr Zhou’s work has shown how to clean up the symmetry of conjugate
quadrature filters and therefore speed up their algorithm time. “As well
as knowing the scheme is perfect, we can show mathematically that it is
correct.” In addition to revealing the mathematical foundation of the
schemes, Dr Zhou’s work has shown how to clean up the symmetry of conjugate
quadrature filters and therefore speed up their algorithm time.
 Using the filters
to sub-band or split a signal into smaller bands of frequencies means that
the different frequency bands can be processed according to their different
characteristics, he said. Using the filters
to sub-band or split a signal into smaller bands of frequencies means that
the different frequency bands can be processed according to their different
characteristics, he said.
 The treatment
of noise, an interference which appears naturally at high frequencies, is
an example. If a signal is separated into sub-bands, noise in the high frequency
can be eliminated without touching the remainder of the signal, he said. The treatment
of noise, an interference which appears naturally at high frequencies, is
an example. If a signal is separated into sub-bands, noise in the high frequency
can be eliminated without touching the remainder of the signal, he said.
 With images,
noise can interfere with the pixels and cause a blurring or blocking effect.
Compression, he said, involves a step beyond digitisation, using part of
the digitised signal. If the digitisation is bad, then the compressed signal
is even worse. With images,
noise can interfere with the pixels and cause a blurring or blocking effect.
Compression, he said, involves a step beyond digitisation, using part of
the digitised signal. If the digitisation is bad, then the compressed signal
is even worse.
 “We want
to keep a balance. If you have a small amount of data, then the speed of
communication is fast. But if you send a large amount of data for the received
message to be the same as the original, then the speed is slow. We need
to achieve a balance.” “We want
to keep a balance. If you have a small amount of data, then the speed of
communication is fast. But if you send a large amount of data for the received
message to be the same as the original, then the speed is slow. We need
to achieve a balance.”
 Dr Zhou has
addressed conferences on the research in North America, Europe, Singapore
and China. Dr Zhou has
addressed conferences on the research in North America, Europe, Singapore
and China.
Principal Investigator
Dr Ding-xuan Zhou : mazhou@cityu.edu.hk

|

![]()
![]() The scientist
attributed with being the Father of the Digital Age, American Claude Shannon,
wrote the blueprint for digital communications in the 1940s. But, said
the CityU project’s Principal Investigator, Dr Ding-xuan Zhou, the
theory could not be implemented.
The scientist
attributed with being the Father of the Digital Age, American Claude Shannon,
wrote the blueprint for digital communications in the 1940s. But, said
the CityU project’s Principal Investigator, Dr Ding-xuan Zhou, the
theory could not be implemented. 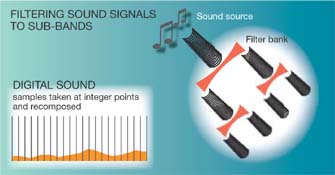
![]()